CNN의 구조로 만든 ResNet은 CNN의 층이 깊어질수록 loss 값이 0이 되는 Vanishing gradient problem(기울기 소실 문제)를 해결하기 위하여 만들어졌다고 한다. 학부 때 ResNet 강연을 들은 적이 있는데, 딥러닝 이미지 인식 파트에서 폭넓게 쓰인다고 한다. 코드 구현과 해석을 위하여 논문을 읽고 정리해보자.
Abstract
초록에서는 뉴럴 네트워크가 깊어질수록 트레인(train) 시키기 어렵다고 문제제기를 한다. 하지만 residual learning(잔차 신경망)을 사용하여 해결할 수 있다고 한다. residual의 사전적 의미는 '여분의', '잔여의'라는 의미이다. residual training을 사용하여 경험적(empirical)으로 좋은 결과를 얻었다고 한다. 이러한 모델을 사용하여, ImageNet 데이터셋을 , VGG NETS보다 8배 깊게 설정하였지만, 오히려 모델의 복잡도는 낮았다고 한다. 그리고 테스트 결과 3.57%에러율을 보였다고 한다. 비전 분야에서 계층의 깊이는 중요한 이슈였지만, ResNet으로 이 문제를 해결하고, 이미지 인식 분야의 ILSVRC & COCO2015 대회에서 우승하였다고 한다.
Introduction
깊은 CNN은 이미지 인식 분야에서 큰 기여를 하였다. 하지만 단순히 층을 깊게 쌓는다고 이미지를 더 잘 인식할까?란 문제에 봉착하게 된다. 이러한 문제는 back-propagation할 때 기울기 소실 문제를 야기한다고 한다. which hamper convergence from the beginning.(기울기 소실 문제는 모델이 처음부터 특정 값에 수렴하는 것을 방해한다.) 이러한 문제는 초기값의 정규화와 중간 계층에서 어느 잡아준다고 한다. with the network depth increasing, accuracy gets saturated(포화시키다.) and then degrades rapidly. 하지만 여전히 계층이 깊어질수록 모델은 포화상태로 바뀌고, degrade는 올라간다고 한다. 이러한 degradation(하락)은 overfitting에 의해서 일어나는 것이 아니다. optimizer를 새로 개발하는 것은 어려운 일이기 때문에, 논문에서는 얇은 층을 깊게 쌓는 모델을 개발하고자 한다. 새로 쌓는 계층을 다시 처음부터 이전 계층과 트레인 시키는 게 아니라 identity로 mapping 해온다. 이 논문에서 저자들은 residual learning을 사용하여, degradation problem을 해결하고자 한다. 최종적으로 학습하려고 하는 계층을 H(x)라고 둔다. 여기서 H(x)를 F(x) + x라 두며, x가 만약에 이상적으로 0이라면 H(X)를 구하기가 매우 쉬울 것이라고 말하고 있다. Identity short-cut으로 H(x)를 구할 수 있는데, Identity shortcut은 복잡한 연산을 요하지 않는다. 즉 이때까지 학습한 계층에 단순히 x를 더하면 되는 것이다. 이러한 performance는 ImageNet과 CIFAR-10에서 좋은 결과를 얻을 수 있었다고 한다. 모델의 계층을 152개 층까지 쌓았다고 한다. 그래도 이것은 VGG nets보다 복잡도가 여전히 더 낮다고 한다.
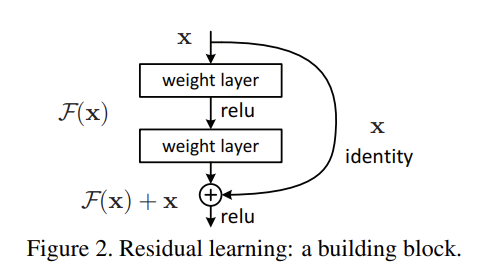
The strong evidence shows that the residual learning principle is generic(포괄적인), and we expect that it is applicable in other vision and non-vison problems. Residal learning의 원리는 단순하며, 이것은 비전 분야와 아닌 분야에서도 폭넓게 사용할 수 있을 것이라 기대한다.
Related Work
For vector quantization, encoding residual vectors is shown to be more effective than encoding original vectors. 이미지 인식에서 VLAD 모델과 Fisher Vector 모두에서 오리지날 벡터보다 residual vector를 사용하였을 때 더 좋은 성능을 보여주었다. PDEs(Partial Differential Equations 편미분) the widely used Multigrid method reformulates the system as subproblems(하위 문제) at multiple scales, where each subproblem is responsible for the residual solution between a coarser and a finer scale. These methods suggest that a good reformulation or preconditioning can simplify the optimization. 컴퓨터 그래픽에서 PDEs의 coaser와 finer scale 문제를 풀 때에, vector보다 residual vector를 사용하여 좀 더 빠르게 연산한 경우를 설명하고 있다.
Short Connections
Shortcut Connections에 관한 연구는 오랫동안 계속 되었다. 예전 연구에서 중간 계층들은 auxiliary(보조의) classifiers에 직접적으로 연결되어서 vanishing gradients problem을 해결하였다. [44] 참고 문헌에서는 inception(시작) layer가 shotcut 가지와 좀 더 깊은 가지를 쳐서 문제를 해결하였다고 한다. 관련 모델에서는 총체적으로 말하면 고속도로 네트워크(highway networks)라고 말할 수 있다. shortcut connection과 그것을 연결해주는 기능들의 결합으로 말할 수 있다. 하지만 이 ResNet은 앞선 작업과 다르게 파라미터와 데이터와 연관성이 전혀 없이, 복잡도를 낮쳐주고 있다.
Deep Residual Learning
Residual Learning
If one hypothesizes that multiple nonlinear layers can asymptotically(점근적으로) approximate the residual function, 여기서도 H(X) = F(X) + x로 점근적으로 해석하여 문제를 쉽게 해결하려고 한다. 더 쌓으려는 계층을 identity mapping(x)로 쌓으면, 얇은 모델과 비교하여 에러가 커지지 않는다고 한다. 만약 identity mapping이 최적이라면, residual learning은 쉽게 0에서 identity mapping까지 쉽게 찾아갈 수 있다. 실제 문제에서 identity mapping이 최적일 확률은 낮다. 최적의 함수에서 identity mapping이 0이 아닐 경우, 모델은 identity mapping을 참고로 애초에 처음부터 학습한 것보다 쉽게 학습할 수 있을 것이다.
Identity Mapping by Shortcuts
residual block

위의 수식은 residual block을 설명해주고 있다. 여기서 x와 y는 각각 input vector와 output vector이다. 수식의 첫 번 째 항은 Residual function을 말하고 있고, 두 번 째 항은 더해지는 identity mapping을 얘기하고 있다.

위의 수식의 시그마는 ReLU함수를 의미한다. biases are omitted(생략) for simplifying notations.bias는 생략한다. 이 모델에서 activation function으로 ReLU 함수를 사용하였다. 첫 번 째 방정식(1)에서, 첫 번째 항과 두 번 째 항은 각 요소별 덧셈(element-wise addition)으로 이루어진다. 이것은 굉장히 중요한 부분이다. 만약에 두 항의 차원이 같지 않으면 방정식(2)와 같이 두 번째 항에 linear projection(W_s)을 곱해준 뒤 더하여 준다.

여기서 linear projection은 단순히 차원을 맞추기 위하여 쓰이는 도구이다.
Network Architectures
Plain model과 Residual model을 대조하여, 실험을 진행하고 한다. Plain Network는 VGG nets처럼 대부분 3X3 Filter를 가지고 있다. 그리고 두 가지 규칙을 가지고 실험을 진행하였다.
(i) output feature map size가 같게끔 한다.
(ii) if the feature map size is halved(반으로 줄어 든), the number of filters is doubled so as to preserve the time complixity for layer. 만약에 feature map size가 반으로 줄어든 다면, 필터의 수는 두배로 하여 시간 복잡도는 유지하게끔 한다.
Residual model은 Plain network의 기반으로 shortcut connection을 삽입하였다. 차원이 증가하더라도 identity mapping을 더 더할 필요는 없다. 결론적으로, 새로운 네트워크는 VGG nets의 연산의 18%만 사용하였고, 복잡도가 훨씬 줄어 들었다.
Implementation
실험의 데이터 셋은 ImageNet으로 진행하였다. 이미지들의 짧은 면들은 사이즈가 재조정 되었다. 그리고 256~480 사이의 샘플로 scale augmentation하였다. 224 x 224짜리 사진(crop : 잘라낸 사진들)들은 이미지나 그것들의 수직으로 뒤집힌 것들에 의해서, 랜덤하게 선택되었다. 픽셀마다 평균값들을 뺀채로, 표준 칼러 augmentation이 적용되었다. batch normalization를 사용하고, 우리는 미니 배치사이즈를 256에서 SGD를 사용하였다. 하이퍼파라미터는 Weight decay 0.0001, momentum 0.9, iteration 60 X 10^4를 사용 하였으며, convolutional form as in [41, 13]에서 차용하였고, 평균 스코어 값은 Multiple scales를 사용하였다.
Experiments
ImageNet Clsassification
1,000개의 클래스로 나누어진 ImageNet 2012로 평가하였다. 1.28 million 갯수의 이미지. 50,000개의 트레인 셋을 진행하였다.
Plain Network
18 ~ 34 plain net에서 비교 실험한 결과 34 층에선는 18층 에서보다 더 높은 validation error를 기록하였다. 표 4를 사용하여 비교 분석해 보았다.

Plain Network에서 BN을 사용하여, 학습을 진행하는데 non-zero variance(변동량)임을 보증하는데도 불구하고, 위와 같은 결과를 얻었다. We also verify that the backward propagated gradients exhibit healthy norms(노름 = 벡터의 크기) with BN. Back propagation을 할 때도, 기울기의 크기가 크게 나타났다. we conjecture(추측하다) that the deep plain nets may have exponentially low convergence rates, which impact the reducing of the training error. Plain network에서는 낮은 수렴값을 보였지만, 그것이 오히려 트레인 할 때, training error를 낮쳐줬다고 생각된다. 그래도 여전히 plain network에서도 경쟁력은 있다고 보았다.
Residual Netwrok
베이스라인은 Plain archintect와 같다. 각 쌍마다 shortcut을 설치하였다. dimension이 높아지면, zero-padding 사용하였다.이전 모델에 비해서 파라미터가 더해지는 일은 없다. 여기서는 34층이 더 좋게 나타났다. 계층이 높아짐으로써 더 좋은 정확도를 보였다. Residual Network를 사용하면 더 깊은 층에서 더 좋은 효과를 나타내는 것을 확인하였다. 수렴 시간도 훨씬 빠르게 진행하였다.

Identity vs Projection Shortcuts
A B C를 비교
(A) dimension을 높이기 위하여, zero-padding shortcuts 사용, 다른 shortcut은 모두 identity shortcut
(B) dimension을 높이기 위하여, Projection shortcuts을 사용, 다른 shortcut은 모두 identity shortcut
(C) 모든 short-cut이 projection shortcut 사용.
Identity shortcut이 더 중요하다는 것을 판단. C의 경우는 사용하지 않기로 하였다.
Deeper Bottleneck(병목 지역) Architectures
bottleneck design에서는 projection shortcut 보다 identity shortcut을 쓰는게 편리하다. 자칫하면 모델 사이즈와 복잡도가 두 배로 늘어날 수 있다.

50 layer에서는 Bottleneck Architecture로 바꾸고,Option C를 채택하였다.
101 - layer and 152-layer ResNets : 세 개의 블록으로 만들어줌. 놀랍게도 층이 깊어져도 여전히 VGG-16/19 nets에 비해서 훨씬 더 복잡도가 낮다. 오히려 모든 평가 항목에서 더 좋은 결과값을 얻었다.
CIFAR-10 and Analysis
CIFAR-10 데이터셋으로 가장 깊은 레이어를 가진 모델의 변화를 관측하려 한다. 최종적으로 레이어가 6n+2 꼴로 만들어 진다. 110 layer에서는 learning rate가 0.1인 경우 초기 값이 수렴이 잘 되지 않아서 0.01로 warm up한 다음에, 0.1로 다시 튜닝하기로 한다. 더 적은 파라미터로 다른 깊고 얇은 모델보다 더 좋은 성능을 보였다. 여기서도 잘 극복한 것으로 보인다. These result support our basic motivation that the residual functions might be generally closer to zero than the non-residal functions. 일반적으로 residual functrion이 non-residual function 보다 0으로 더 잘 optimization 되었다.
Exploring Over 1000 layers
계층을 지나치게 많이 쌓으면 결론적으로 오버 피팅이 일어난다. 만약 미래에서 강한 정규화를 통해 이 문제를 더 잘 극복할 수 있을지 모른다.
Object Detection on PASCAL and MS COCO
Object Detection에서도 ResNet이 VGG-16보다 더 좋은 성능을 보였다.

